I’ve finished a course at Aarhus University called Algorithm Engineering taught by Gerth Brodal. The course description reads:

The participants must at the end of the course be able to:

  • Construct and analyze performance experiments for algorithm implementations.
  • Construct and implement algorithms optimized towards efficient usage of the underlying computer architecture.

We implemented algorithms for 3 seperate projects. The projects are written in C++, and we use CMAKE to manage the build process. We used PAPI to collect data from the hardware (level 1 and 2 cache misses, branch mispredictions etc.), and finally plottet the results using Gnuplot.

Some of the interesting findings include how big an impact memory layout has on the running time of your (theoretically) fast algorithm. When implementing binary search, something as simple as changing the ordering of the searched array yields large performance gains.

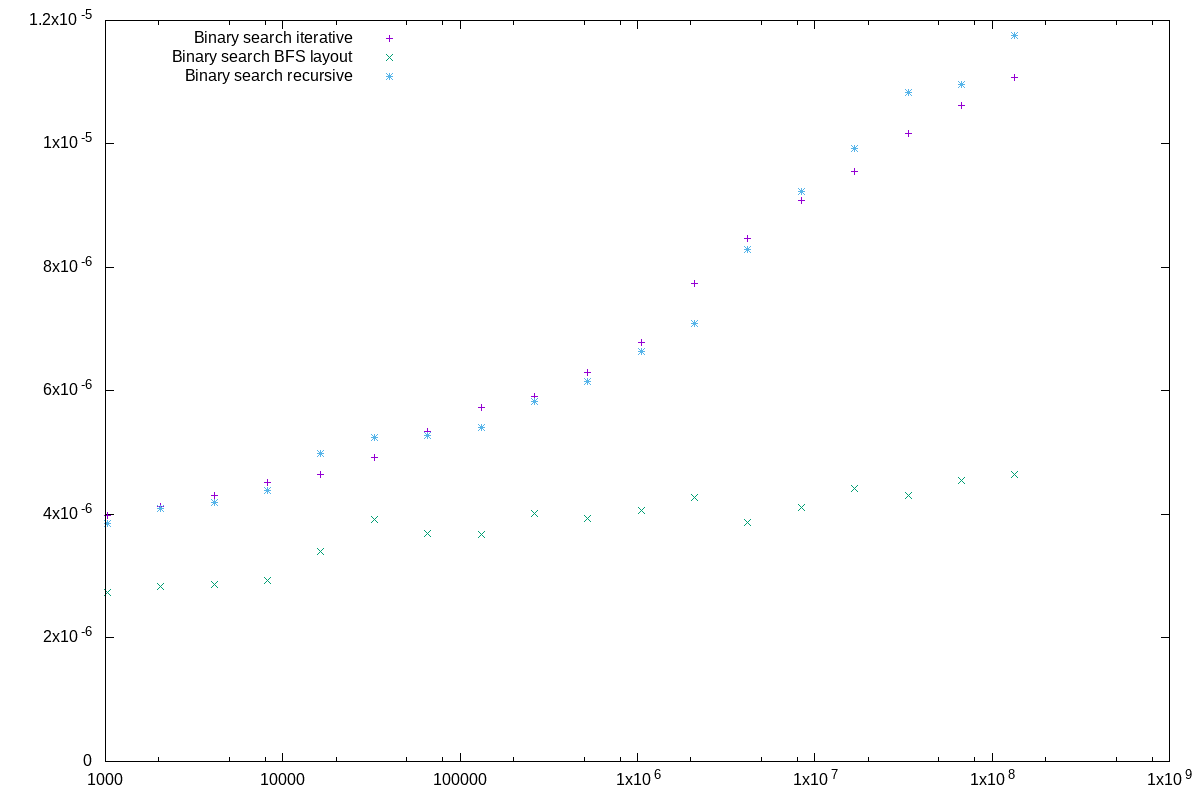
Comparison binary search

Plotting the different algorithms against each other immediately shows how engineering an algorithm toward efficient hardware usage has a big impact on performance.

Another finding was that sometimes doing more results in faster algorithms. Another project involved matrix multiplication. One major improvement was transposing the matrix to multiply with. This allows for sequential memory access in both matrices, which is a lot faster than accessing indices that are far apart (because they are different rows in the matrix). This means that doing more work (most CPU instructions) is a lot faster than having to wait for the memory. Even for matrices of size \(100 x 100\), the extra \(\mathcal{O}(n^2)\) required to transpose the matrix is worth the investment. If the same matrix is to be using in multiple calculations, the overhead will be even less significant. This is especially true since (naive) matrix multiplication require \(\mathcal{O}(n^3)\) multiplications.

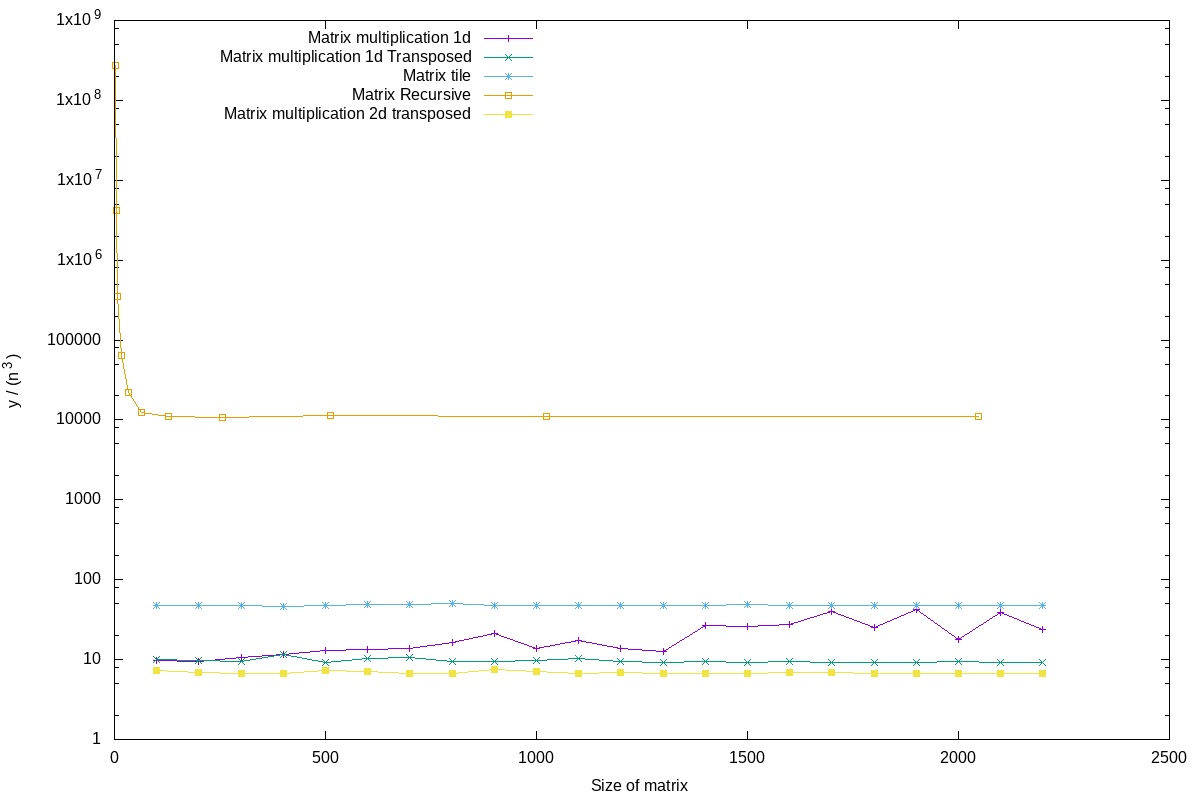
Comparison matrix multiplication

Different tricks to achive faster matrix multiplication. Note that transposing matrices before multiplying is significantly faster.